Transformer-XL

Learning Transformer-XL

Transformer-XL模型&&代码

Posted by biggan on December 20, 2019

Transformer-XL 学习笔记

1 论文：

Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context （卡耐基梅隆大学&&谷歌大脑）

2 简介

2.1 为什么是XL

XL指“extra-long”，意为”超长“。基于Transformer的预训练模型Bert规定输入的序列长度不超过512，Transformer-XL相对于Transformer，能够对更长的序列进行建模。

2.2 解决的问题

对于超长的序列，Transformer结构需要根据固定的最大长度，将其拆分成几段，然后对各段分开处理。这将带来两个问题，① 上下文碎片化 ：由于各段分开处理，段之间信息不能共享，尤其是一段中前一部分序列，不能利用到其上文的信息（它的上文在上一段）。② 超长依赖建模 ：因为最大长度（段长）的限制，使得模型不能够捕获超过最大长度的长期依赖关系。而Transformer-XL就解决了这两个问题。

2.3 如何解决的

即，Transformer-XL 的要点/贡献

  • 基于状态重用的分段循环机制

Transformer-XL结构中引入了循环的概念，前一个片段的信息会被存储起来，在当前片段的处理中会重用前一段中的隐状态，通过此方式在段之间建立循环连接。

  • 新的位置编码方案

论文提出了一种简单有效的相对位置编码方式。这种方式的相对位置编码直接作用在每一层的attention分数的计算上，而非加在网络输入层的词向量上。

3 摘要

Transformer 网络具有学习更长期依赖性的潜力，但这种潜力往往会受到语言建模中上下文长度固定的限制。因此，我们提出了一种叫做 Transformer-XL 的新神经架构来解决这一问题，它可以在不破坏时间一致性的情况下，让 Transformer 超越固定长度学习依赖性。具体来说，它是由片段级的循环机制和全新的位置编码策略组成的。我们的方法不仅可以捕获更长的依赖关系，还可以解决上下文碎片化的问题。Transformer-XL 学习到的依赖性比 RNN 学习到的长 80%，比标准 Transformer 学到的长 450%，无论在长序列还是短序列中都得到了更好的结果，而且在评估时比标准 Transformer 快 1800+ 倍。此外，我们还提升了多个任务的当前最佳结果，在 enwiki8 上 bpc 从 1.06 提升至 0.99，在 text8 上从 1.13 提升至 1.08，在 WikiText-103 上困惑度从 20.5 提升到 18.3，在 One Billion Word 上从 23.7 提升到 21.8，在 Penn Treebank （不经过微调的情况下）上从 55.3 提升到 54.5。 当仅在WikiText-103上进行训练时，Transformer-XL能够生成具有数千个字符的合理连贯的文本。我们还提供了Tensorflow和PyTorch的代码，预训练模型和超参数。

4 模型

4.1 基于状态重用的分段循环（Segment-Level Recurrence with State Reuse）

（1）将一串很长的文本序列，按固定长度划分成若干段（segment）。在处理某一段时，该段的每一层都会接收两个输入：

  • 该段前一层的输出；
  • 前一段前一层的输出，这是模型建模超长依赖的关键 。

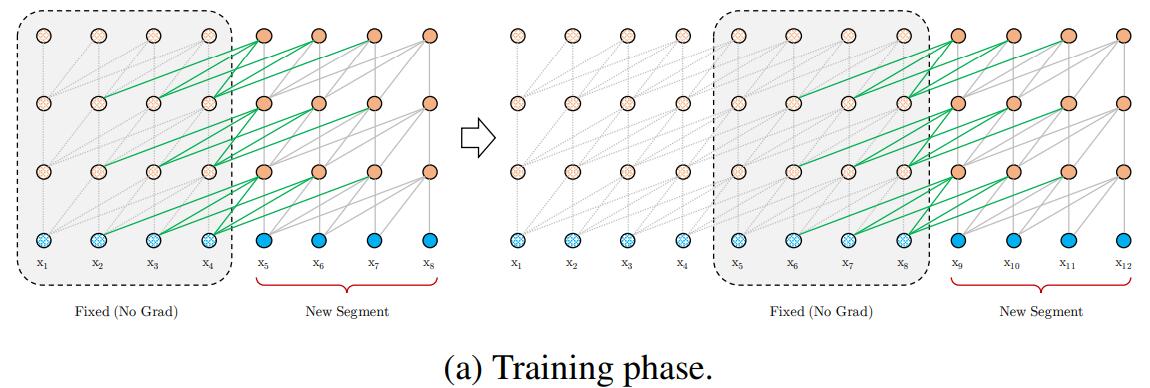
TIM截图20191210194324

我的理解：

在这种循环结构下，某一段某个词在某一层的向量表示（隐状态）是由前一段和当前段内所有词在前一层的中的状态表示加权求和得到。注意：

①不要受上图中绿色箭头的影响，认为只有绿色箭头部分参与计算，当然我们也可以把网络设计成绿色箭头所表示的结构。

②对于要预测下一个词的语言建模任务，我们应该mask一个词后面的所有词（transformer decoder做法），即只由前一个段的词和当前段内某词及其前面的词的表示加权求和得到当前词的下一个向量表示。实际代码中的做法是：将某词后面的词对该词的注意力分数替换为“-inf”，经过softmax后，这些词对应的权重将为0。

③这种结构下，每次都是重用（保存）前一个段的表示。实际上，我们不仅可以保存前一个段，我们也可以保存前若干段，甚至若干个单元（词）。

④第一段没有前一段，代码实际的做法不同于RNN中随机初始化$h_0$，而是在第一段各层的状态计算中，只使用了第一段中存在的词，即没有使用任何前一段的信息。

⑤网络输入的词向量层是网络的第一层，即词向量层作为第一个decoder层的前一层。

（2）通过此循环机制，可建模的最大的依赖长度随网络层数呈线性增长，即为O(N×L)。如下图所示：

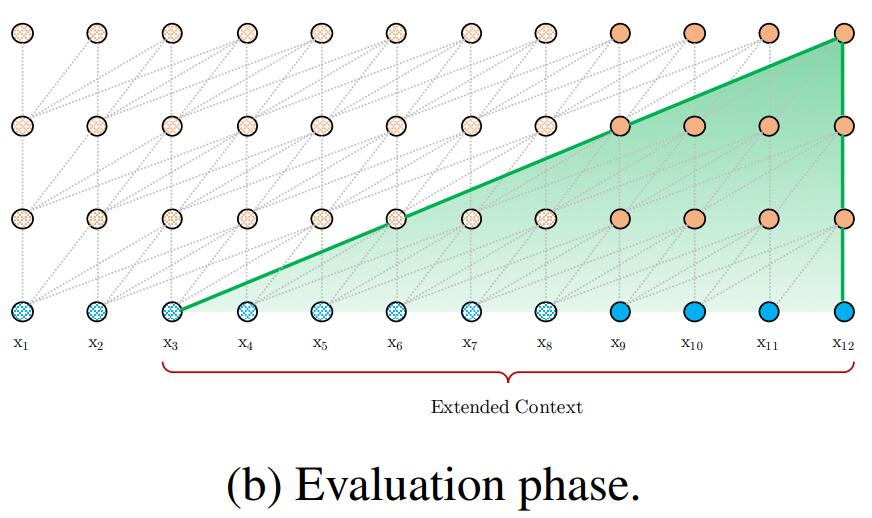
TIM截图20191210211034

计算过程：

令长度为L的两个连续段分别为$\mathbf{s}{\tau}=\left[x{\tau,1}, \cdots, x_{\tau, L}\right]$和$\mathbf{s}{\tau+1}=\left[x{\tau+1,1}, \cdots, x_{\tau+1, L}\right]$。 第$\tau$段$s_{\tau}$的第n层隐状态序列表示为$\mathbf{h}{\tau}^{n} \in \mathbb{R}^{L \times d}$，其中d为隐藏层维度。第$\tau +1$段$s{\tau +1}$的第n层隐状态计算如下： \(\begin{aligned} \widetilde{\mathbf{h}}_{\tau+1}^{n-1} &=\left[\mathrm{SG}\left(\mathbf{h}_{\tau}^{n-1}\right) \circ \mathbf{h}_{\tau+1}^{n-1}\right] \\ \mathbf{q}_{\tau+1}^{n}, & \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}=\mathbf{h}_{\tau+1}^{n-1} \mathbf{W}_{q}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{k}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{v}^{\top} \\ \mathbf{h}_{\tau+1}^{n}=& \text { Transformer-Layer }\left(\mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}\right) \end{aligned}\) $其中，SG(\cdot)函数表示\text{stop-gradient }，即SG内的值不进行梯度反向传播。\left[h_{u}^{\circ} h_{v}\right]表示沿序列长度方向将两个隐藏序列连接起来。$

4.2 相对位置编码（Relative Positional Encodings ）

不同段的相同位置应区分对待，即$x_{\tau,j}$和$x_{\tau+1,j}$之间存在位置差异，应该使用不同的位置编码。

Transformer通过在网络的输入层，将单词的词向量和位置编码直接相加的方式，以将序列的绝对位置信息编码到模型中。然而，Transformer-XL并没有将绝对位置信息嵌入到输入层初始的词向量中，而是进行相对位置编码，在每层的注意力分数的计算时嵌入相对位置信息。

注意力分数的计算不再是$A_{i,j}=(W_qq_i)^{\top}W_kk_j=q_i^{\top}W_q^{\top}W_kk_j$，实际计算方式如下： \(\begin{aligned} \mathbf{A}_{i, j}^{\mathrm{rel}} &=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(b)} \\ &+\underbrace{u^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{v^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(d)} \end{aligned}\) 该式中的$E_{x_{i}}$、$E_{x_{j}}$分别为上式中的$q_i$和$k_j$，即需要计算注意力的两单词的向量表示；

R是一个表示相对位置向量的正弦编码矩阵；

$u \in \mathbb{R}^{d}$和$v \in \mathbb{R}^{d}$均是一个可学习的参数。

(a)式为没有添加位置信息的原始注意力分数，论文中的说法是（content-based addressing）

(b)式为关于内容的位置偏差（content-dependent positional bias）

(c)式为全局的内容偏差（global content bias），全局体现在与q无关

(d)式为全局的位置偏差（global positional bias）

4.3 完整的计算过程

一个单头的N层Transformer-XL的计算过程如下：

$For \ n = 1, . . . , N:$ \(\begin{aligned} \widetilde{\mathbf{h}}_{\tau}^{n-1} =&\left[\mathrm{SG}\left(\mathbf{h}_{\tau-1}^{n-1}\right) \circ \mathbf{h}_{\tau}^{n-1}\right] \\ \mathbf{q}_{\tau}^{n}, \mathbf{k}_{\tau}^{n}, \mathbf{v}_{\tau}^{n}=& \mathbf{h}_{\tau}^{n-1} \mathbf{W}_{q}^{n \top}, \tilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{k, E}^{n \top}+\widetilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{v}^{n \top} \\ \mathbf{A}_{\tau, i, j}^{n}=& \mathbf{q}_{\tau, i}^{n \top} \mathbf{k}_{\tau, j}^{n}+\mathbf{q}_{\tau, i}^{n \top} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j} +u^{\top} \mathbf{k}_{\tau, j}^n+v^{\top} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j} \\ \mathbf{a}_{\tau}^{n}=& \text { Masked-Softmax }\left(\mathbf{A}_{\tau}^{n}\right) \mathbf{v}_{\tau}^{n} \\ \mathbf{o}_{\tau}^{n}=&\left. \text { LayerNorm (Linear ( }\left.\mathbf{a}_{\tau}^{n}\right)+\mathbf{h}_{\tau}^{n-1}\right) \\ \mathbf{h}_{\tau}^{n}=&\text { Positionwise-Feed-Forward }\left(\mathbf{o}_{\tau}^{n}\right) \end{aligned} \\\)

5 代码

However，官方提供的代码中，对位置信息的编码和注入提供了多种方式，且不同于论文中所给的计算公式。不同方式主要有两点区别：①硬编码or软编码；②输入层注入绝对位置编码信息or注意力层注入相对位置编码信息。

  1. 方式1（硬编码+相对位置编码） \(A_{\tau, i, j}^{n}= (q_{\tau, i}^{n}+w\_bias)^{\top}k_{\tau, j}^{n}+(q_{\tau, i}^{n}+b\_bias)^{\top}(R_{i-j}W_{k, R}^{n \top})\) 其中，$R$是表示相对位置向量的正弦编码矩阵（硬编码方式）；$w_bias$、$b_bias$是一个d_head维的可学习的参数向量，在一个head内，对所有段，所有层，所有词共享；但在不同head中不同。

  2. 方式2（软编码+相对位置编码） \(A_{\tau, i, j}^{n}= (q_{\tau, i}^{n}+w\_bias^n)^{\top}k_{\tau, j}^{n}+(q_{\tau, i}^{n}+w\_bias^n)^{\top}R_{i-j}^n+r\_bias_{i-j}^n\) 其中，$R^n$为第n层的相对位置向量构成的矩阵（软编码方式，可学习），且$R^n$在不同head中也不共享；$r_bias^n$为第n层的相对位置偏置构成的向量，且$r_bias^n在不同head中也不共享$；$w_bias^n$在不同层不同head中同样不共享。

  3. 方式3（硬编码+绝对位置编码）

    在网络输入层，将绝对位置编码（硬编码方式）直接加在当前段和前一段的词向量上；注意这里的绝对位置仅仅是当前段和前一段构成的这两段中绝对位置，并非所有段中的绝对位置。

    Attention计算同transformer中的做法$A_{\tau, i, j}^{n}= q_{\tau, i}^{n}k_{\tau, j}^{n}$。

  4. 方式4（软编码+绝对位置编码）

    在网络输入层，将绝对位置编码（软编码方式，可学习）直接加在当前段和前一段的词向量上；注意，这里的绝对位置也是对两段而言的，且不同层使用不同的绝对位置编码。

    Attention计算同transformer中的做法$A_{\tau, i, j}^{n}= q_{\tau, i}^{n}k_{\tau, j}^{n}$。

    相关代码

    ###  定义位置编码
if self.attn_type == 0:  # default attention
    self.pos_emb = PositionalEmbedding(self.d_model)
    self.r_w_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))
    self.r_r_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))
elif self.attn_type == 1:  # learnable
    self.r_emb = nn.Parameter(torch.Tensor(
        self.n_layer, self.max_klen, self.n_head, self.d_head))
    self.r_w_bias = nn.Parameter(torch.Tensor(
        self.n_layer, self.n_head, self.d_head))
    self.r_bias = nn.Parameter(torch.Tensor(
        self.n_layer, self.max_klen, self.n_head))
elif self.attn_type == 2:  # absolute standard
    self.pos_emb = PositionalEmbedding(self.d_model)
elif self.attn_type == 3:  # absolute deeper SA
    self.r_emb = nn.Parameter(torch.Tensor(
        self.n_layer, self.max_klen, self.n_head, self.d_head))
   
#### 模型前向过程
if self.attn_type == 0: # default
    pos_seq = torch.arange(klen-1, -1, -1.0, device=word_emb.device, 
                           dtype=word_emb.dtype)  # [klen] 逆序编号
    if self.clamp_len > 0:
        pos_seq.clamp_(max=self.clamp_len)
    pos_emb = self.pos_emb(pos_seq)
   
    core_out = self.drop(word_emb)
    pos_emb = self.drop(pos_emb)
   
    hids.append(core_out)
    for i, layer in enumerate(self.layers):
        mems_i = None if mems is None else mems[i]
        core_out = layer(core_out, pos_emb, self.r_w_bias,
                self.r_r_bias, dec_attn_mask=dec_attn_mask, mems=mems_i)
        hids.append(core_out)
elif self.attn_type == 1: # learnable
    core_out = self.drop(word_emb)
    hids.append(core_out)
    for i, layer in enumerate(self.layers):
        if self.clamp_len > 0:
            r_emb = self.r_emb[i][-self.clamp_len :]
            r_bias = self.r_bias[i][-self.clamp_len :]
        else:
            r_emb, r_bias = self.r_emb[i], self.r_bias[i]
   
        mems_i = None if mems is None else mems[i]
        core_out = layer(core_out, r_emb, self.r_w_bias[i],
                r_bias, dec_attn_mask=dec_attn_mask, mems=mems_i)
        hids.append(core_out)
elif self.attn_type == 2: # absolute
    pos_seq = torch.arange(klen - 1, -1, -1.0, device=word_emb.device,
                           dtype=word_emb.dtype)
    if self.clamp_len > 0:
        pos_seq.clamp_(max=self.clamp_len)
    pos_emb = self.pos_emb(pos_seq)
   
    core_out = self.drop(word_emb + pos_emb[-qlen:])
   
    hids.append(core_out)
    for i, layer in enumerate(self.layers):
        mems_i = None if mems is None else mems[i]
        if mems_i is not None and i == 0:
            mems_i += pos_emb[:mlen]
        core_out = layer(core_out, dec_attn_mask=dec_attn_mask,
                         mems=mems_i)
        hids.append(core_out)
elif self.attn_type == 3:
    core_out = self.drop(word_emb)
   
    hids.append(core_out)
    for i, layer in enumerate(self.layers):
        mems_i = None if mems is None else mems[i]
        if mems_i is not None and mlen > 0:
            cur_emb = self.r_emb[i][:-qlen]
            cur_size = cur_emb.size(0)
            if cur_size < mlen:
                cur_emb_pad = cur_emb[0:1].expand(mlen-cur_size, -1, -1)
                cur_emb = torch.cat([cur_emb_pad, cur_emb], 0)
            else:
                cur_emb = cur_emb[-mlen:]
            mems_i += cur_emb.view(mlen, 1, -1)
        core_out += self.r_emb[i][-qlen:].view(qlen, 1, -1)
   
        core_out = layer(core_out, dec_attn_mask=dec_attn_mask,
                         mems=mems_i)
        hids.append(core_out)

6 参考

https://github.com/kimiyoung/transformer-xl

https://www.lyrn.ai/2019/01/16/transformer-xl-sota-language-model/

CATALOG
    FEATURED TAGS
    tools RNNs Pytorch Trick Text Classification file NMT IE others Bert ELmo ERNIE Transformer-XL
    FRIENDS